STAT 4830: Numerical Optimization for Data Science and Machine Learning - Damek Davis
Table of contents | Course overview | View on Github

Slide 1: Lecture 0 — Introduction

Purpose: Set the goal for today and the course.

Why Optimization?

To quote Joshua Achiam (OpenAI):

If you want to know something deep, fundamental, and maximally portable between virtually every field: study mathematical optimization.

Joshua Achiam's tweet about mathematical optimization

What did students think?

Khush's tweet

Slide 2: Course abstract

Purpose: Orient you to what this course is about.

Optimization is the modeling language in which modern data science, machine learning, and sequential decision-making problems are formulated and solved numerically. This course will teach you how to formulate these problems mathematically, choose appropriate algorithms to solve them, and implement and tune the algorithms in PyTorch. Tentative topics include:

Slide 3: Prerequisites, format, deliverables

Purpose: Make expectations concrete.

Prerequisites

Format

Deliverables (final project)

Slide 4: A brief history of optimization

Purpose: Place “optimization for ML” in a larger arc.

EVOLUTION OF OPTIMIZATION
========================

1950s                1960s-1990s              2000s                  TODAY
├─────────────────┐  ├────────────────┐  ┌────────────────┐  ┌─────────────────┐
│ LINEAR PROGRAM. │  │ CONVEX OPTIM.  │  │ SOLVER ERA     │  │ DEEP LEARNING   │
│ Dantzig's       │──│ Interior-point │--│ CVX & friends  │──│ PyTorch         │
│ Simplex Method  │  │ Large-scale    │  │ "Write it,     │  │ Custom losses   │
└─────────────────┘  └────────────────┘  │  solve it"     │  │ LLM boom        │
       │                    │            └────────────────┘  └─────────────────┘
       │                    │                   │                    │
       ▼                    ▼                   ▼                    ▼
 APPLICATIONS:        APPLICATIONS:       APPLICATIONS:        APPLICATIONS:
 • Logistics         • Control           • Signal Process    • Language Models
 • Planning          • Networks          • Finance           • Image Gen
 • Military          • Engineering       • Robotics          • RL & Control

Slide 5: Why PyTorch?

Purpose: Explain why this course is centered on PyTorch.

Slide 6: Preview — spam classification becomes optimization

Purpose: Show the conversion from an ML task to an optimization problem.

We start with a task: classify email as spam or not spam.

We turn that into an optimization problem by specifying:

  1. Features: how an email becomes a vector $x$.
  2. Decision variables: weights $w$ that map features to a prediction.
  3. Objective: a loss function $L(w)$ (cross-entropy).
  4. Solve: choose $w$ by minimizing $L(w)$ using gradient descent.

Slide 7: Features — email $\mapsto$ vector $x$

Purpose: Convert emails to features.

Example feature set (here $x \in \mathbb{R}^5$):

We must choose some way of representing an email as a vector. Here we use a rudimentary feature set that counts the number of exclamation marks, the number of urgent words, the number of suspicious links, the hour the email was sent, and the length of the email.

In modern approaches, features are typically learned rather than hard-coded.

Slide 8: Prediction rule (decision variable = $w$)

Purpose: Show how $w$ produces a prediction.

We score an email by a weighted sum, then convert it to a probability:

\[p_w(x) = \sigma(x^\top w).\]

Spam Classification Process

Slide 9: Sigmoid = score $\mapsto$ probability

Purpose: Explain the probability map we use for binary classification.

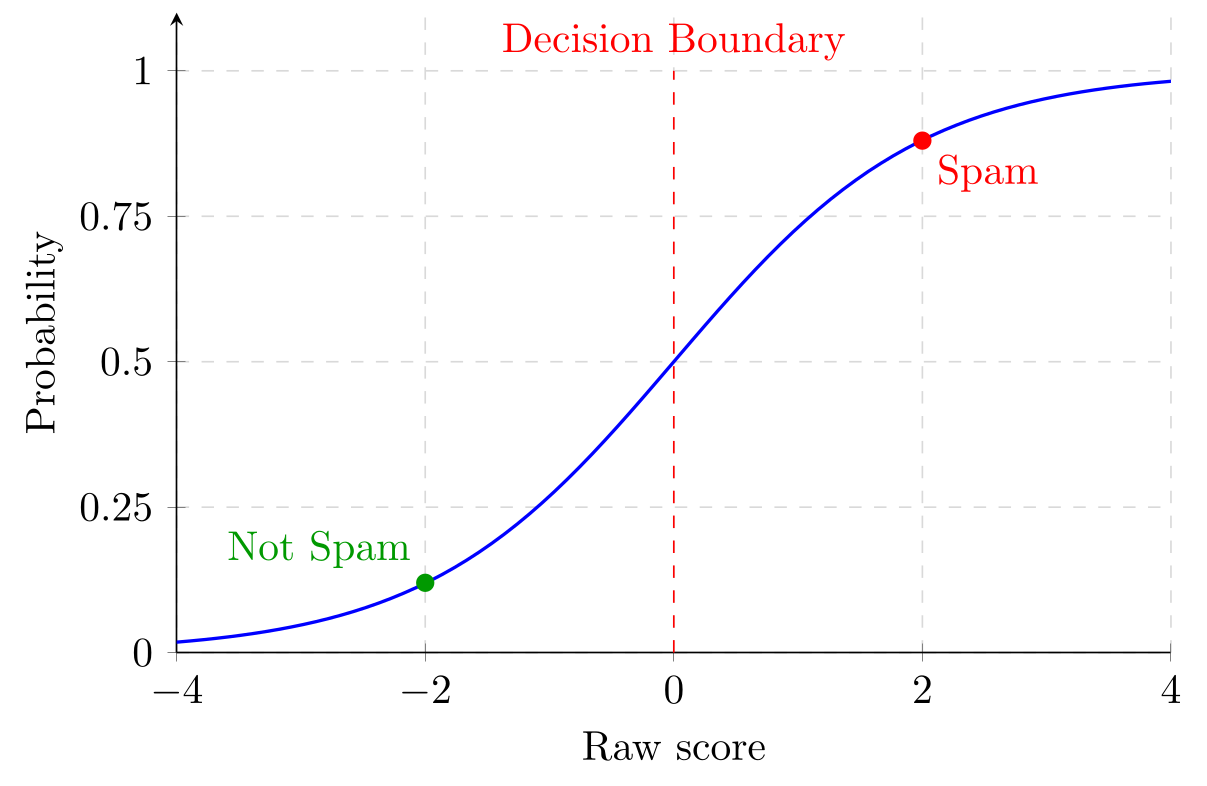
Sigmoid Function

Slide 10: Objective (cross-entropy) = add up penalties over positive and negative samples

Purpose: Show how the two curves combine into one objective.

For each email $i$, the model predicts $p_i=\sigma(x_i^\top w)$, interpreted as “probability of spam.”

Let $P={i:y_i=1}$ (spam examples) and $N={i:y_i=0}$ (not-spam examples). We minimize the average loss

\[L(w)=\frac{1}{n}\left[\sum_{i\in P}-\log(p_i)+\sum_{i\in N}-\log(1-p_i)\right].\]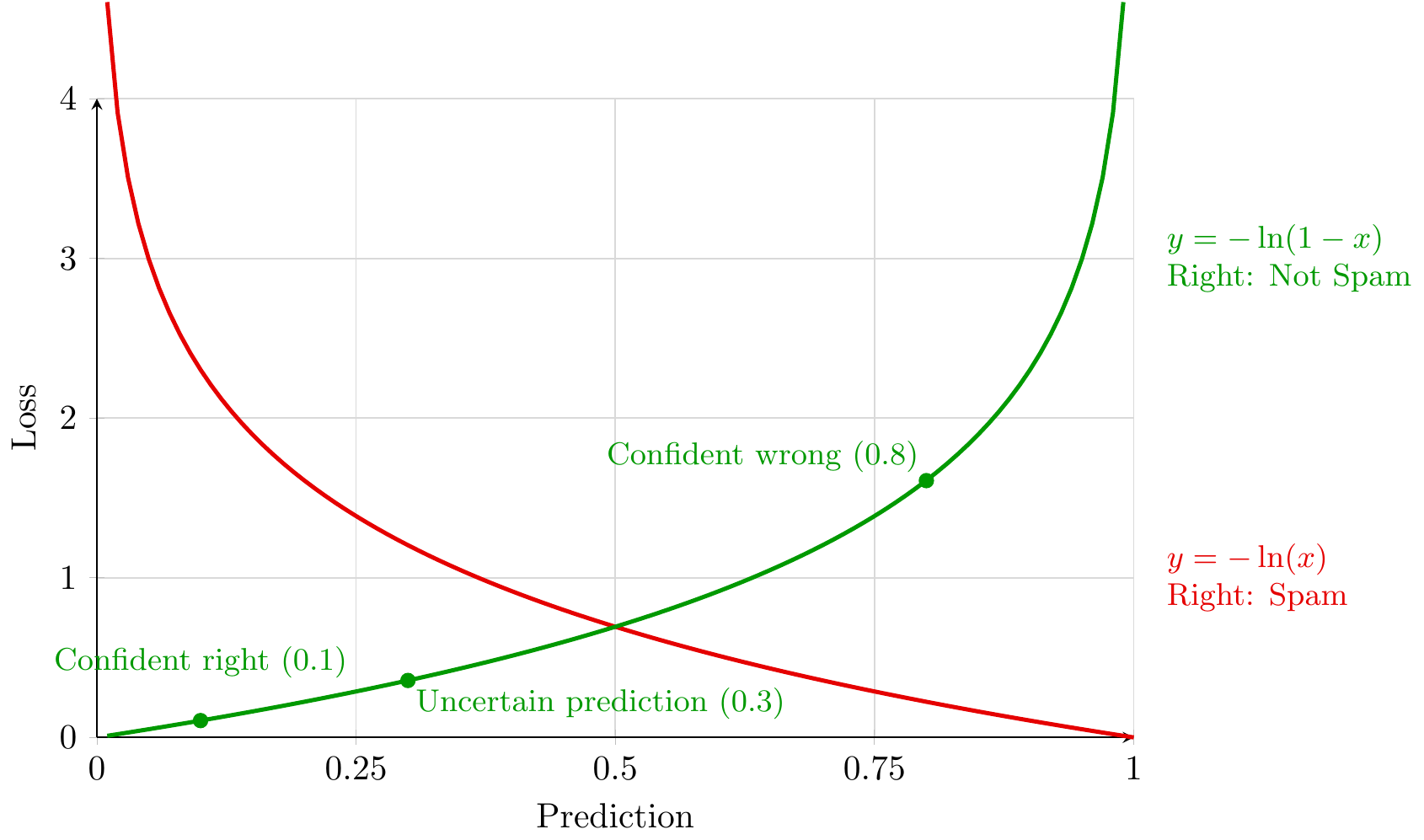

Cross-Entropy Loss

Slide 11: Gradients and gradient descent

Purpose: Explain why the negative gradient direction is decreases the loss.

The gradient collects partial derivatives:

\[\nabla L(w)=\left(\frac{\partial L}{\partial w_1},\ldots,\frac{\partial L}{\partial w_d}\right).\]

The first-order approximation is

\[L(w+\Delta)\approx L(w)+\langle \nabla L(w),\Delta\rangle.\]

Taking $\Delta=-\eta \nabla L(w)$ gives the decrease-to-first-order calculation

\[L(w-\eta \nabla L(w)) \approx L(w) - \eta \|\nabla L(w)\|^2.\]

So gradient descent uses

\[w \leftarrow w - \eta \nabla L(w), \qquad w_j \leftarrow w_j - \eta \frac{\partial L}{\partial w_j}.\]

Here $\eta>0$ is the learning rate (stepsize).

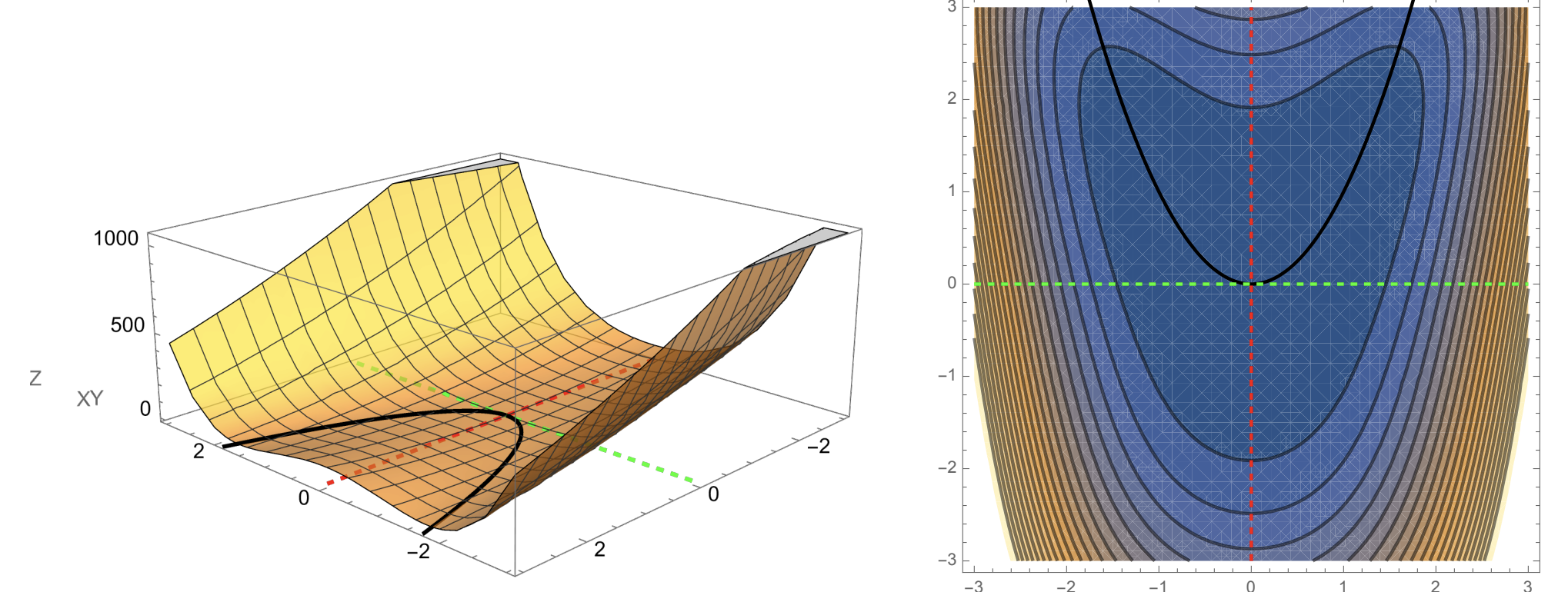
Slide 12: A picture (useful, but limited)

Purpose: Give a cartoon picture of optimization landscape.

Gradient descent visualization showing path from high point to minimum

This visualization is a simplification. In higher dimensions, the optimization landscape can have local minima, saddle points, and ravines.

Saddle point example. Saddle point example in an optimization landscape

Ravine example. Ravine example: narrow curved valley in an optimization landscape

Slide 13: Implementing the update in PyTorch

Purpose: Show that the code is implementing the math update.

In PyTorch, loss.backward() computes $\nabla L(w)$ and stores it in weights.grad. The update line is the same as $w \leftarrow w - \eta \nabla L(w)$.

weights = torch.randn(5, requires_grad=True)
learning_rate = 0.01

for _ in range(1000):
    predictions = spam_score(features, weights)
    loss = cross_entropy_loss(predictions, true_labels)

    loss.backward()

    with torch.no_grad():
        weights -= learning_rate * weights.grad
        weights.grad.zero_()

Two details:

Slide 14: Numerical results (diagnostics vs generalization)

Purpose: Introduce several useful plots when training a model.

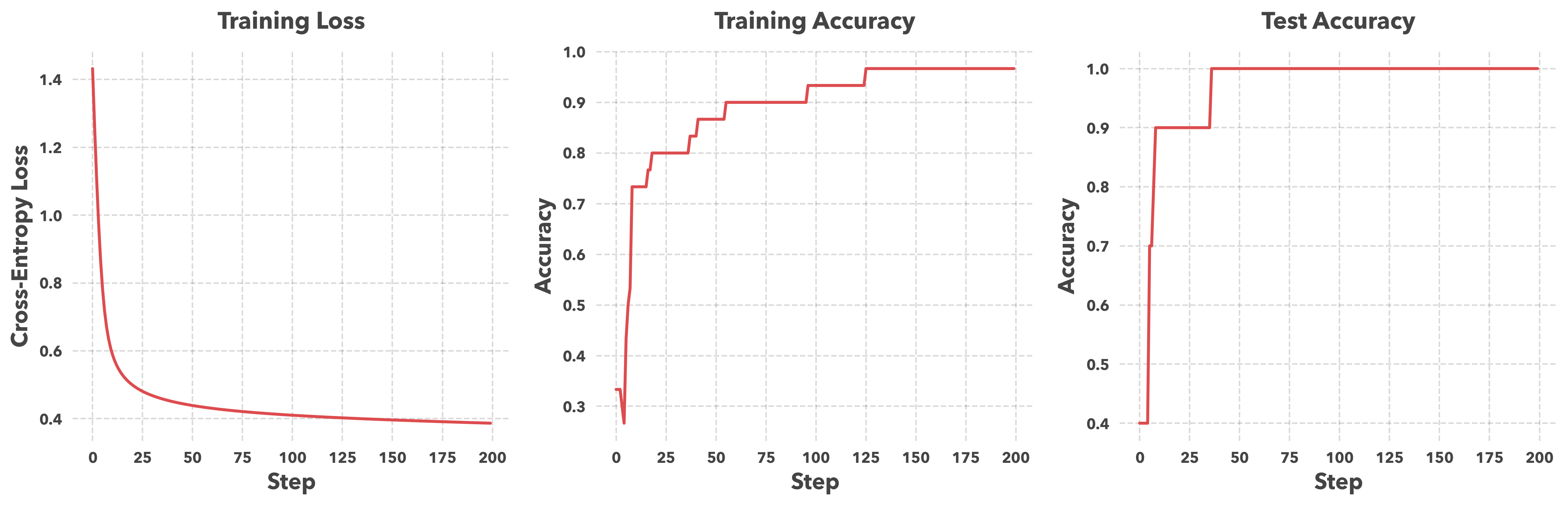
Loss curves

Slide 15: What, how, and why of PyTorch (autodiff)

Purpose: Explain how PyTorch computes gradients: recorded composition + chain rule.

If you build a scalar loss using PyTorch operations, PyTorch records the operations used to compute it. When you call backward(), it applies the chain rule through that recorded computation and produces derivatives with respect to variables that have requires_grad=True.

One-dimensional example. Fix $y$ and define

\[f(x)=(x^2-y)^2.\]

Write $h(x)=x^2$ and $g(z)=(z-y)^2$, so $f=g\circ h$. The chain rule gives

\[f'(x)=g'(h(x))h'(x)=2(x^2-y)\cdot 2x = 4x(x^2-y).\] 
y = 3.0
x = torch.tensor(2.0, requires_grad=True)

f = (x**2 - y)**2
f.backward()
print(x.grad.item())  # 4*x*(x**2 - y)

The payoff: you can change the model or the loss and keep the same training loop.

Slide 16: Tentative course structure + learning outcomes

Purpose: Give you the roadmap and what you should be able to do by the end.

Course structure (high-level)

By the end of the course, you should be able to

  1. Formulate optimization problems (variables, objectives, constraints) in math and code.
  2. Implement and debug gradient-based training loops in PyTorch.
  3. Choose reasonable algorithms and hyperparameters, and recognize bad tuning.
  4. Benchmark methods in a way that is not misleading.
  5. Have basic systems awareness (compute, memory, data loading bottlenecks).
  6. Produce a portfolio-quality project (clean repo, working implementation, short write-up).

Slide 17: Final project structure

Project instructions: STAT-4830-project-base

ITERATIVE DEVELOPMENT PROCESS    PROJECT COMPONENTS
=============================    ==================

┌─────────────────┐  ┌─────────────────┐  ┌────────────────────┐
│  INITIAL SETUP  │  │  DELIVERABLES   │  │  PROJECT OPTIONS   │
│  Teams: 3-4     ├──┤  • GitHub Repo  │  │ • Model Training   │
│  Week 2 Start   │  │  • Demo         │  │ • Reproducibility  │
└───────┬─────────┘  │  • Final Paper  │  │ • Benchmarking     │
        │            │  • Slide Deck   │  │ • Research Extend  │
        │            └───────┬─────────┘  │ • ...              │
        │                    │            └────────────────────┘
        │                    ▼
        │            ┌─────────────────┐  BIWEEKLY SCHEDULE
        ▼            │    FEEDBACK     │  ════════════════
┌─────────────────┐  │ PEER REVIEWS:   │  Week 3:  Report
│   IMPLEMENT     │◀─┤ • Run Code      │  Week 4:  Slides Draft
│ • Write Code    │  │ • Test Demo     │  Week 5:  Report
│ • Test & Debug  ├─▶│ • Give Feedback │  Week 6:  Slides Draft
│ • Document      │  │                 │  Week 7:  Report
└─────────────────┘  │ PROF MEETINGS:  │  Week 8:  LIGHTNING TALK
                     │ • Week 3 Scope  │  Week 9:  Report
                     │ • Week 7 Mid    │  Week 10: Slides Draft
                     │ • Week 11 Final │  Week 11: Report
                     └─────────────────┘  Week 12: Slides Draft
                                          Week 13: Final Report
DEVELOPMENT WITH LLMs                     Week 14: Final Presentation
• Write & review reports, documentation
• Develop & test code (verify outputs!)
• Regular commits with clear documentation

Slide 18: Be systematic with megaprompts (coding agents)

Purpose: Treat prompting like engineering: a stable spec + iterative refinement.

Why megaprompts now?

Getting started with a megaprompt: some ideas

This will be an element of your final deliverable.