Lecture 10 Cheat Sheet: Benchmarking Optimizers

I. Introduction: The Optimizer Comparison Problem

• The Problem: Determining if Optimizer A is truly “better/faster” than Optimizer B for complex deep learning models is difficult. Naive comparisons (loss curves, final values) are often misleading.
• Why? Performance depends on subtle interactions: optimizer + specific workload + hyperparameter selection process.
• Context: We’ve studied optimizers (SGD, Momentum, Adam, etc.) and theory (L6, L7, L9 mean estimation, NQM). Now we address practical empirical comparison.

II. Challenge 1: Defining “Speed” - Crossing Curves

• Ambiguity: Simply plotting validation loss vs. time/steps is ill-posed. Curves frequently intersect, meaning which optimizer is “ahead” changes throughout training.
• Evidence (Dahl et al., 2023, Fig 1):
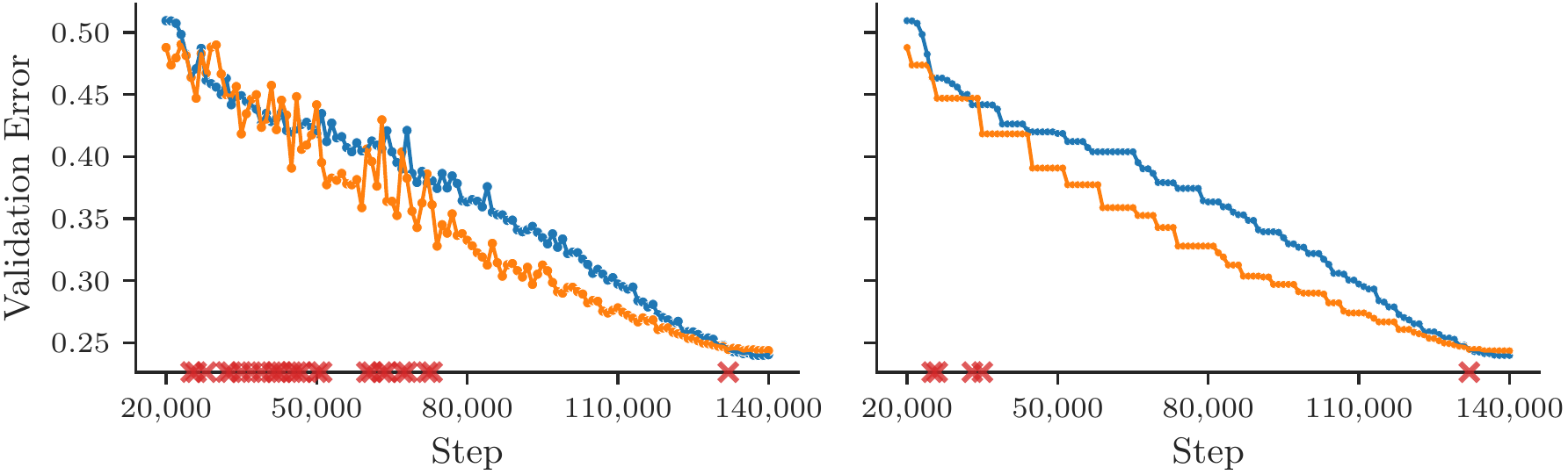  • (Representational Thumbnail)
  • Shows: Raw validation curves cross (left); even “best-so-far” (running minimum) curves cross (right). No clear winner from curve shape alone.
  • Quote: “Figure 1: A direct comparison of training curves is ill-posed if they intersect. Left: The validation error for two different runs… Right: The best validation error obtained so far by each curve… the curves intersect multiple times…” (Dahl et al., 2023, p. 10)
• Solution: Time-to-Result (TTR)
  • Definition: Measure the time (wall-clock/steps on standard hardware) required to first reach a pre-defined target performance value (e.g., target validation error).
  • Benefit: Provides a single, unambiguous endpoint for comparing speed. (Dahl et al., 2023, Sec 4.1).

III. Challenge 2: The Hyperparameter Tuning Trap

• Core Issue: The Hyperparameter Tuning Protocol is arguably the biggest confounder. Optimizer performance comparisons are meaningless without specifying how HPs were chosen.
• The Protocol includes:
  • Search Space: Which HPs (LR, $\beta_1, \beta_2, \lambda, \epsilon$, schedule params…) are tuned & over what ranges?
  • Budget: How many tuning trials are allowed?
  • Method: How are trials sampled (random, grid, etc.)?
• Concept: Optimizer Inclusion Hierarchy (Choi et al., 2019b, Def 1):
  • Definition: $M \subseteq N$ if N can simulate M (e.g., SGD $\subseteq$ Momentum).
  • Theory: With infinite tuning budget, N should perform $\ge$ M.
  • Practical Question: Does this hold with realistic, finite tuning budgets? (Often not, if tuning is unfair/incomplete).
• Evidence 1: Tuning Protocol Reverses Rankings (Choi et al., 2019b, Fig 3):
  • (Representational Thumbnail)
  • Shows: Prior finding (Adam < Momentum) occurred with limited tuning (LR only). When more HPs were tuned fairly for both optimizers, performance became comparable, contradicting the earlier result.
  • Quote: “Figure 3: Tuning more hyperparameters removes the differences in test error between optimizers observed by Wilson et al. (2017). Tuning a subset… is sufficient to equalize performance… More extensive hyperparameter tuning… improves results for all optimizers and still does not produce any differences…” (Choi et al., 2019b, p. 7)
• Evidence 2: Protocol Sensitivity (Choi et al., 2019b, Fig 4):
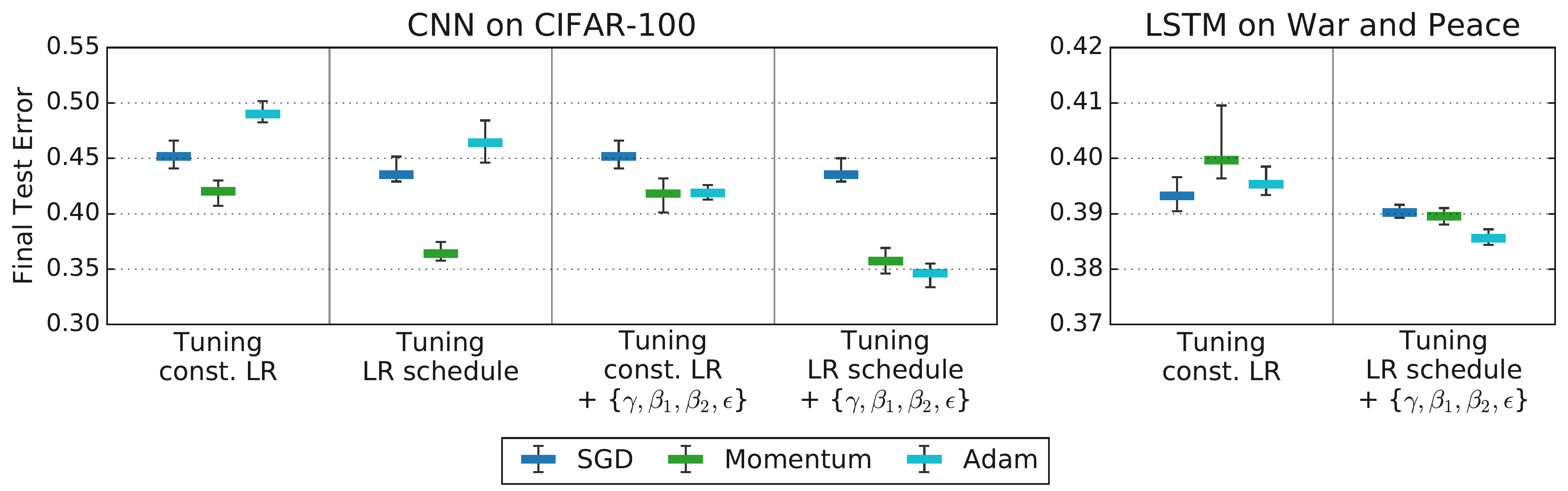  • (Representational Thumbnail)
  • Shows: Optimizer rankings change significantly based on which HPs are included in the tuning protocol (compare left vs right bars per task). Rankings align with theory ($SGD \subseteq Momentum \subseteq Adam$) only under comprehensive tuning.
  • Quote: “Figure 4: Tuning more hyperparameters changes optimizer rankings from Schneider et al. (2019) to rankings that are consistent with the inclusion relationships…” (Choi et al., 2019b, p. 8)
• CRITICAL TAKEAWAY: The Optimizer + its FULL Tuning Protocol (Search Space, Budget, Method) is the unit being compared. Specifying only the optimizer name is insufficient. (Choi et al., 2019b, Sec 5).

IV. Detailed Tuning Strategies from Sources

• Goal: Understand specific mechanics of tuning used in benchmarks/studies.

• 1. AlgoPerf Benchmark Tuning Rulesets (Dahl et al., 2023; Kasimbeg et al., 2024)
  • A. External Tuning:
    • Simulates: Limited parallel tuning budget.
    • Submitter Provides: HP Search Space (or OptList).
    • Benchmark Runs: N trials (e.g., 5) per study via quasi-random search. Selects best trial based on fastest time to validation target. Repeats M times (e.g., 5 studies) w/ different seeds.
    • Score: Median TTR to test target across studies (using the best-validation trial from each study).
  • B. Self-Tuning:
    • Simulates: Fully automated algorithm.
    • Submitter Provides: Algorithm (no external HPs). All tuning must be internal, “on the clock”.
    • Benchmark Runs: Once per study. Larger time budget (e.g., 3x). Repeats M times (e.g., 5 studies) w/ different seeds.
    • Score: Median TTR to test target across studies.
• 2. Choi et al. (2019b) Experimental Tuning:
  • Goal: Show protocol choice changes results.
  • Compared Protocols:
    • “Limited Tuning”: Mimicked prior work => LR only tuned; other HPs fixed at defaults.
    • “Comprehensive Tuning”: Tuned multiple HPs: LR, schedule params, Momentum coeff, Adam $\beta_2, \epsilon$. Used quasi-random search, fixed budget (10-100 trials). Used log-uniform search spaces (explicit ranges in App D). Selected based on final validation perf. (Crucially decoupled Adam $\alpha_0, \epsilon$ tuning).
  • Finding: Moving Limited $\rightarrow$ Comprehensive changed optimizer rankings.

V. A Solution: Rigorous Benchmarking Principles (AlgoPerf Example)

• Goal: Standardized framework for fair comparison. AlgoPerf (Dahl et al., 2023).
• Key Principles:
  1. Metric: Time-to-Result (TTR) using pre-defined targets.
  2. Hardware: Standardized, fixed hardware.
  3. Workloads: Diverse suite + Held-out variants (test robustness).
  4. Isolation: Strict API limits submissions to algorithm changes only.
  5. Tuning Rules: Explicit External vs. Self-Tuning rulesets.
  6. Scoring: Aggregate using Performance Profiles.
• Understanding Performance Profiles:
  • (Representational Thumbnail - e.g., External Tuning)
  • X-axis ($\tau$): Slowdown factor relative to best on that workload ($\tau \ge 1$).
  • Y-axis (% Workloads): Fraction solved within factor $\tau$ of best time.
  • Interpretation: Higher / Further Left = Better. More problems solved faster relative to best.
  • Quote: “In the performance profiles (b, d), each line represents a submission. A step at $\tau$ indicates that, for one workload, this submission reaches the target within $\tau$ times the runtime of the fastest submission…” (Kasimbeg et al., 2024, p. 4)

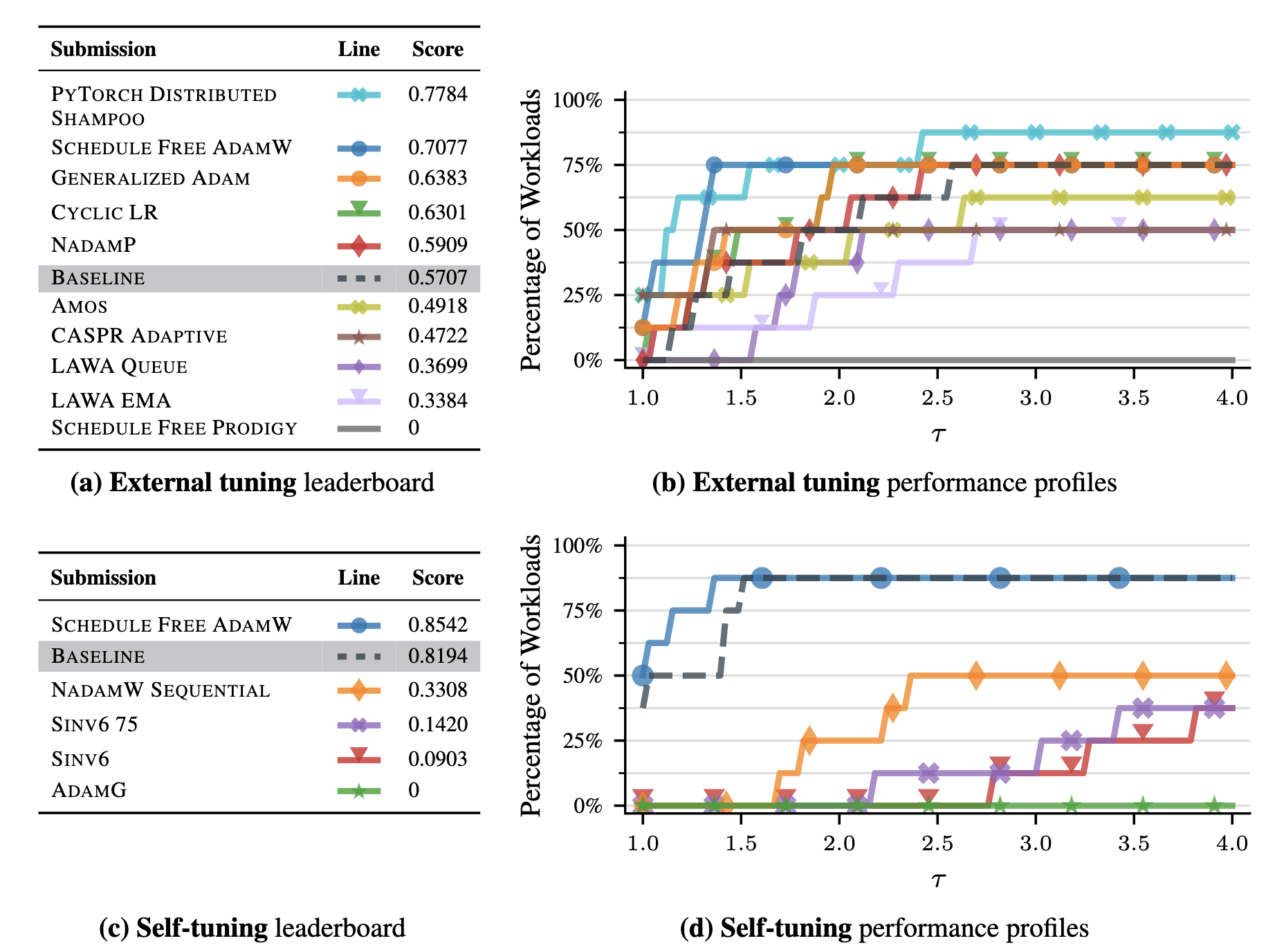
VI. What We Learned: AlgoPerf Competition Results (Kasimbeg et al., 2024)

• Overall Outcome (Kasimbeg et al., 2024, Fig 1):
  • (Representational Thumbnail)
  • Shows: Leaderboards (a, c) & Profiles (b, d). Benchmark differentiates optimizers.
  • Winners: Distributed Shampoo (External), ScheduleFreeAdamW (Self-Tuning).
• Finding 1: Advanced Preconditioning Works (External):
  • Who: Distributed Shampoo (non-diagonal preconditioning).
  • What: ~28% faster avg. wall-clock vs NadamW baseline when fairly tuned.
  • Significance: Shows practical benefit of advanced methods beyond Adam variants in a controlled setting. (Kasimbeg Sec 3).
• Finding 2: Hyperparameter-Free Progress (Self-Tuning):
  • Who: ScheduleFreeAdamW.
  • What: ~10% faster than external tuning baseline on common tasks, using zero external tuning.
  • Significance: Promising progress towards automated training. (Kasimbeg Sec 3.2).
• Finding 3: Robustness is Crucial:
  • Evidence: Kasimbeg Table 1 shows many failures (inf, NaN, †, ‡) for various submissions.
  • (Representational Thumbnail)
  • Shows: Winners were reliable across workloads, not necessarily fastest everywhere. Robustness key to high aggregate score.
  • Quote: “Table 1: Normalized submission runtimes… inf denotes… did not reach… target… NaN indicates an error… † indicates… held-out score is ignored… ‡ indicates… base workload score is ignored…” (Kasimbeg et al., 2024, p. 5)
• Other Lessons: Fair cross-framework (JAX/PyTorch) comparison needs effort (Kasimbeg Sec 4). Benchmark design involves cost/benefit trade-offs (Kasimbeg Sec 5.1).

VII. Conclusion

• Bottom Line: Comparing optimizers reliably REQUIRES standardized benchmarks.
• Reason: Must control for workload, hardware, speed definition (TTR), and explicitly account for the full tuning protocol. Naive comparisons are misleading.
• Actionable Insight: Treat Optimizer + Tuning Protocol as the indivisible unit of evaluation. Report protocols meticulously or use benchmarks.