DeepSeek-Prover-V2 overview
TLDR
DeepSeek-Prover-V2 uses DeepSeek-V3 to generate proof plans and decompose formal math problems into subgoals for Lean 4. A 7B prover model attempts to formally prove these subgoals. Training data pairs the DeepSeek-V3 plan with the completed Lean proof, but only for theorems where all subgoals were successfully solved and verified. Reinforcement learning fine-tunes prover models using Group Relative Policy Optimization (GRPO), a binary success reward, and a structural consistency reward that enforces inclusion of planned subgoals. The method achieved state-of-the-art results on the MiniF2F benchmark.
Method
The system trains Lean 4 theorem provers using a specific data synthesis pipeline followed by reinforcement learning.
Synthetic Data Generation:
The process takes a formal theorem statement in Lean 4. DeepSeek-V3 produces (1) a natural language proof plan (chain-of-thought) and (2) a corresponding Lean 4 proof skeleton. This skeleton uses have statements, which introduce intermediate propositions within the proof, to define subgoals from the plan. Proofs for these subgoals are left as sorry placeholders; sorry is a Lean keyword allowing code with incomplete proofs to compile. Figure 2 illustrates this decomposition output.

A 7-billion parameter prover model (DSPv2-7B) attempts to replace each sorry with valid Lean tactics. A strict filter selects data: only if the 7B model successfully proves every single subgoal, resulting in a complete Lean proof verified by the compiler, is the instance kept. For these successful instances, the original natural language plan is paired with the complete, verified Lean 4 proof ({NL Plan, Verified Lean Proof}) to form the cold-start dataset.
Subgoals from these successful decompositions also generate curriculum learning tasks (Figure 3) used in model training. These tasks involve proving subgoals directly or with preceding subgoals provided as premises. Providing premises aims to train contextual reasoning, mirroring lemma usage in proofs, though the paper does not present evidence isolating the benefit of this structure compared to proving subgoals independently.

Reinforcement Learning:
Models, initialized via supervised fine-tuning, are trained using Group Relative Policy Optimization (GRPO). GRPO is a policy gradient method (see Basic facts about policy gradients for an intro to policy gradients) updating policies based on relative proof success rankings within a sampled batch, differing from methods using explicit value functions. The primary reward is binary (+1 for verified proof). An auxiliary structural consistency reward encourages alignment with the DeepSeek-V3 plan early in training by “enforcing the inclusion of all decomposed have-structured lemmas in the final proof.”
Generation Modes: Distinct prompts (Appendix A) elicit two modes: non-CoT (concise Lean code) for efficiency, and CoT (code with NL comments) for interpretability/accuracy. The non-CoT prompt requests code completion directly, while the CoT prompt first asks for a proof plan before generating the commented code.
Evaluation
The DeepSeek-Prover-V2 models were evaluated on Lean 4 formalizations using several benchmarks. Test sets were reserved for evaluation only.
Established benchmarks included MiniF2F, ProofNet, and PutnamBench. MiniF2F contains 488 elementary math problems from competitions (AIME, AMC, IMO) and the MATH dataset, previously formalized; the paper uses the standard valid/test splits, incorporating miniF2F-valid into training curriculum. ProofNet offers 371 undergraduate pure math problems (analysis, algebra, topology) translated from Lean 3 formalizations; the evaluation uses the ProofNet-test split. PutnamBench uses problems from the Putnam Mathematical Competition (1962-2023) covering diverse undergraduate topics, formalized in Lean 4; the evaluation used 649 problems compatible with Lean 4.9.0.
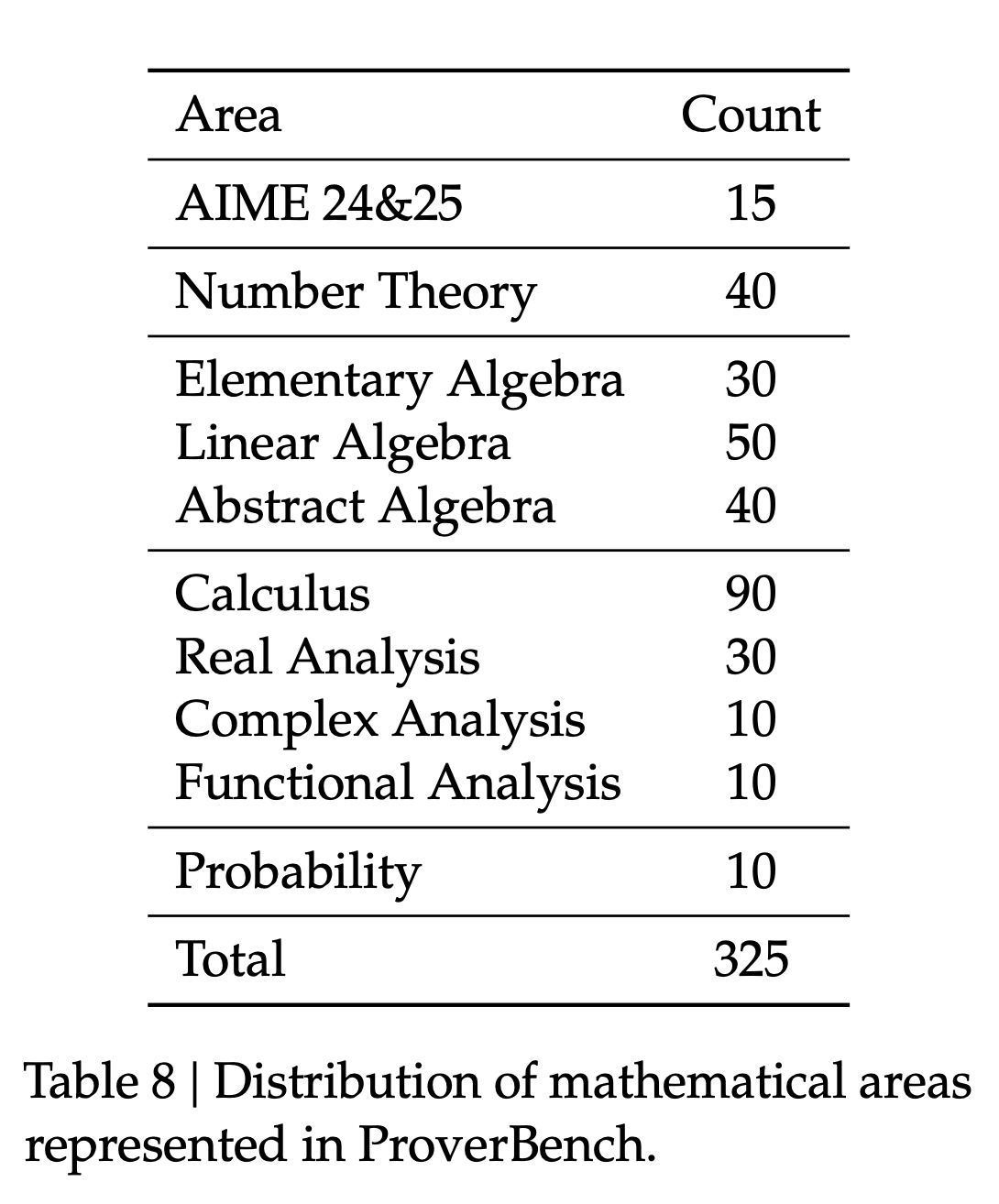
The authors also introduced ProverBench, a new 325-problem benchmark formalized for this work. It aims to span high-school competition and undergraduate levels. It includes 15 recent AIME problems (2024-25) focused on number theory and algebra (Table 7 details selection), filtering out geometry and combinatorics. The remaining 310 problems come from textbooks and tutorials covering number theory, algebra (elementary, linear, abstract), calculus, analysis (real, complex, functional), and probability (Table 8 shows distribution). ProverBench is available via the paper’s GitHub repository.

. |
|
Results
-
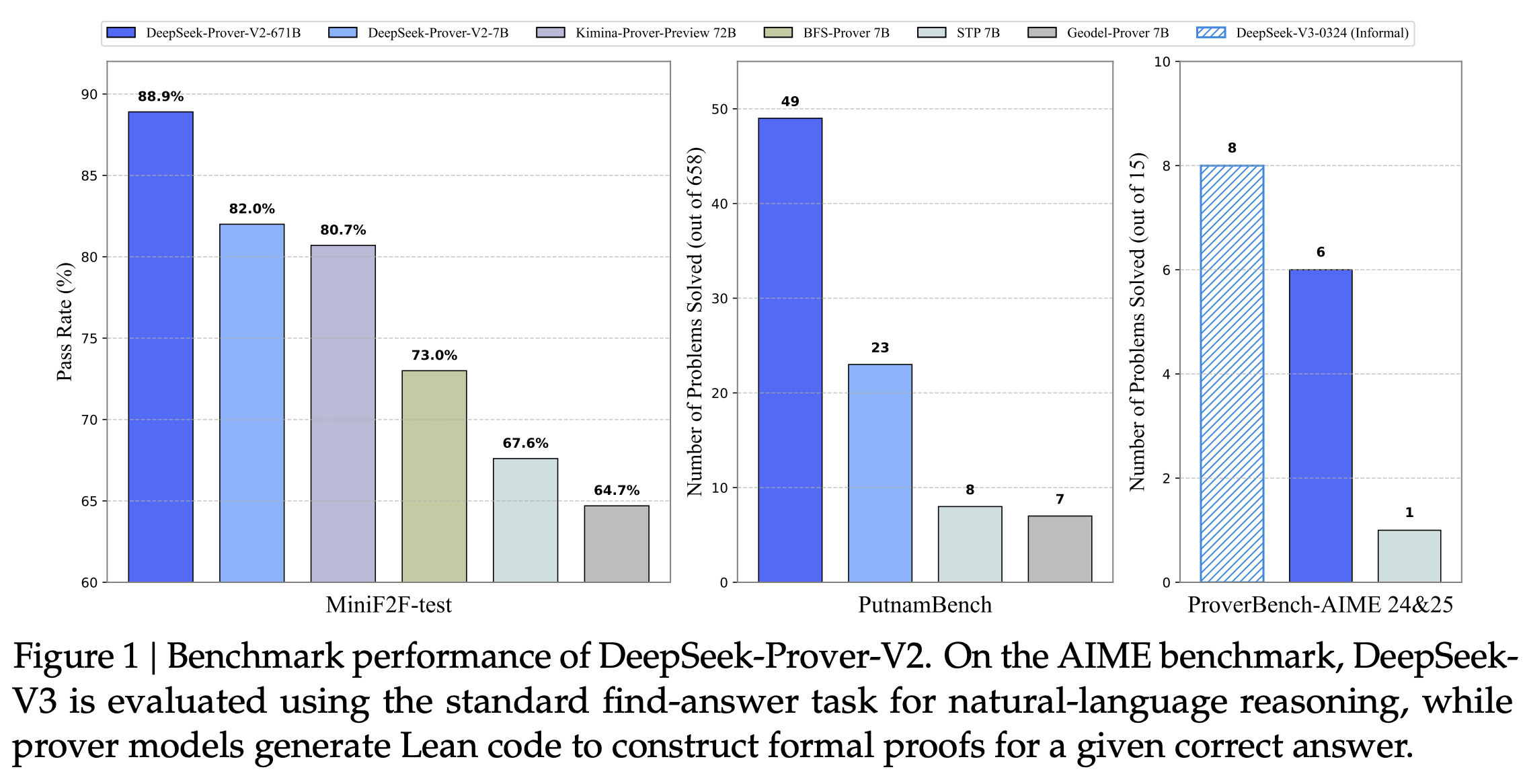
Performance: On MiniF2F-test (Olympiad math), DSPv2-671B (CoT) achieved 88.9% Pass@8192 and 82.4% Pass@32, exceeding prior state-of-the-art (Table 1). On PutnamBench (competition math), it solved 49/658 problems (Pass@1024, Table 4). Figure 1 shows benchmark graphs.
-
ProverBench: On the AIME subset of the authors’ new benchmark, DSPv2-671B (CoT, formal proof) solved 6/15 problems, versus 8/15 solved by DeepSeek-V3 via informal reasoning. (Table 6).
-
Skill Discovery: DSPv2-7B (non-CoT) solved 13 PutnamBench problems missed by the 671B model. It used specific Lean tactics (
Cardinal.toNat,Cardinal.natCast_inj). These tactics are needed because Lean strictly distinguishes types.Cardinalrepresents set size abstractly, whileNatrepresents natural numbers. Even for finite sets, proving properties that rely onNatarithmetic (like specific inequalities) might require explicitly converting aCardinalsize to aNatusingCardinal.toNator using lemmas likeCardinal.natCast_injto relate equalities across types. Standard arithmetic tactics may not automatically bridge this type gap. The 7B model’s RL process apparently favored strategies requiring these tactics for certain problems. (Appendix B examples).